Ciąg Fibonacciego to ciąg liczb, w którym każda liczba jest sumą dwóch poprzednich liczb w ciągu. Zaczyna się on od 0 i 1, a kolejne liczby w ciągu to 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 i tak dalej. Ciąg Fibonacciego ma wiele zastosowań w matematyce, informatyce, finansach a w szczególności samej naturze.
Jednak ciąg Fibonacciego ma pewną zaskakującą cechę, a mianowicie powtarzalność i schematyczność. Z niewiadomych przyczyn nie dowiemy się tego z publikacji naukowych, co jest dość zaskakujące.
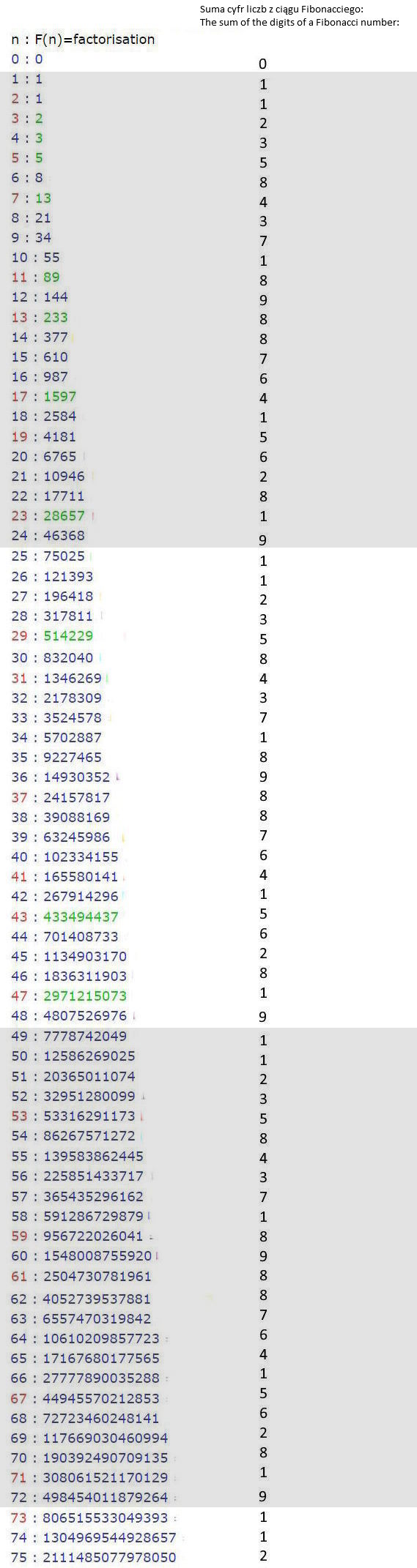
Ciąg Fibonacciego w 50% składa się z liczb należących do wzorów 6n-1 i 6n+1. Ciekawostką jest że wzory te tworzą również wszystkie liczby pierwsze, liczby przypierwsze i wartości p, q i n klucza publicznego w algorytmie szyfrowania RSA. Dodatkowo ciąg Fibonacciego składa się w 50% z liczb pierwszych i przypierwszych, czyli iloczynów i kwadratów liczb pierwszych. Liczby pierwsze w ciągu Fibonacciego od piątej pozycji jego indeksu (czyli liczby 5) mają zawsze sumę cyfr wynoszącą 1, 4, 5 lub 8. W ciągu Fibonacciego (od 5 pozycji jego indeksu (liczby 5) brak zatem liczb pierwszych których suma cyfr wynosi 2 i 7. Patrząc na ciąg Fibonacciego zauważamy że im dalej postępuje to jest w nim coraz więcej liczb przypierwszych, a mniej liczb pierwszych.
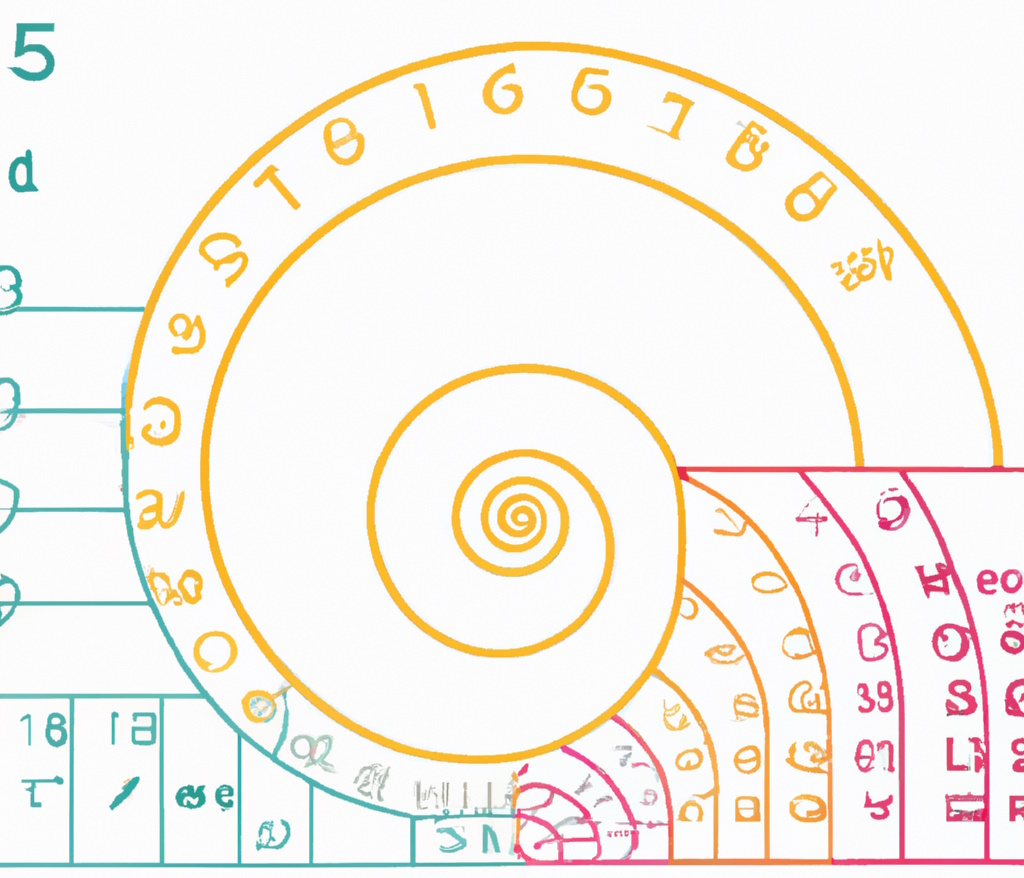
24-elementowa sekwencja liczb
Na obrazku poniżej widzimy że ciąg Fibonacciego tworzy 24-elementową sekwencję liczb należących do wzorów:
6n, 6n+1 gdzie n >= 0 oraz 6n-4, 6n-3, 6n-2, 6n-1 gdzie n > 0

24-elementowa sekwencja sum cyfr
W ciągu Fibonacciego powtarza się też systematycznie (od pierwszej pozycji jego indeksu) znowu 24-elementowa sekwencja sum cyfr każdej liczby. Ta 24-elementowa powtarzająca się sekwencja sum cyfr w ciągu Fibonacciego (licząc od 1. indeksu (liczby 1) rozkłada się według następującej kolejności:
1,1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9
Dodatkowo suma dwóch poprzednich „sum cyfr” liczb Fibonacciego jest równa sumie cyfr kolejnej liczby Fibonacciego i rozkłada się także według w/w kolejności.
Artykuł bazuje na informacjach ze strony marsik.co.pl/ciag-fibonacciego.