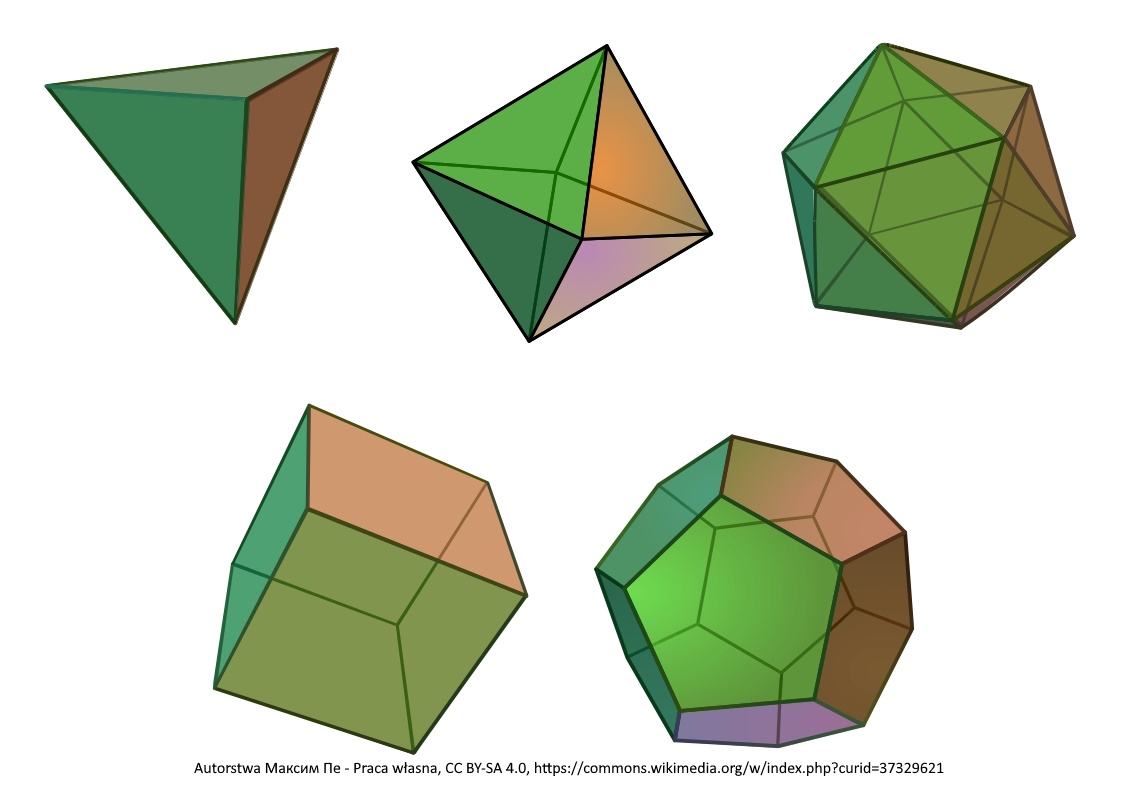
Wielościan foremny, znany również jako bryła platońska, to jeden z najbardziej podstawowych i fascynujących obiektów w matematyce. Są to obiekty, które posiadają identyczne ściany, krawędzie i wierzchołki. Istnieje tylko pięć takich kształtów: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Każdy z nich ma swoje unikalne właściwości i zastosowania, od nauki i matematyki po sztukę i architekturę. Ten artykuł daje wgląd w fascynujący świat idealnych wielościanów foremnych.
Definicja
Wielościan foremny to wielościan, który spełnia następujące warunki:
- Wszystkie jego ściany są identycznymi, przystającymi wielokątami foremnymi.
- W każdym wierzchołku spotyka się taka sama liczba ścian.
- Wielościan jest symetryczny, tzn. można go obrócić wokół środka tak, aby wyglądał tak samo z każdej perspektywy.
- Jest bryłą wypukłą.
Pięć Idealnych Wielościanów Foremnych
Czworościan
Najprostszym wielościanem foremnym jest czworościan (tetraedr), który składa się z czterech równobocznych trójkątów. Każde trzy trójkąty spotykają się w jednym wierzchołku. Czworościan ma 4 wierzchołki, 6 krawędzi i 4 ściany.
Autorstwa Oryginał: Kjell André Vector: DTR – Vectorisation of Tetrahedron.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2231463
Sześcian
Sześcian (heksaedr), czyli bryła, którą wszyscy dobrze znamy, składa się z sześciu kwadratów. W każdym wierzchołku spotykają się trzy kwadraty. Sześcian ma 8 wierzchołków, 12 krawędzi i 6 ścian.
Autorstwa Oryginał: Kjell André Vector: DTR – Praca własna, oparta o: Hexahedron.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2231470
Ośmiościan
Ośmiościan (oktaedr) składa się z ośmiu równobocznych trójkątów. W każdym wierzchołku spotykają się cztery trójkąty. Ośmiościan ma 6 wierzchołków, 12 krawędzi i 8 ścian.
Autorstwa User:Stannered – Vectorisation of Image:Octahedron.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1742116
Dwunastościan
Dwunastościan (dodekaedr) składa się z dwunastu regularnych pięciokątów. W każdym wierzchołku spotykają się trzy pięciokąty. Dwunastościan ma 20 wierzchołków, 30 krawędzi i 12 ścian.
Autorstwa DTR, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2231561
Dwudziestościan
Dwudziestościan (ikosaedr) składa się z dwudziestu równobocznych trójkątów. W każdym wierzchołku spotyka się pięć trójkątów. Dwudziestościan ma 12 wierzchołków, 30 krawędzi i 20 ścian.
Autorstwa DTR – Oryginał: Cyp Vector: DTR, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2231553
Dlaczego tylko pięć?
Można by zadać pytanie, dlaczego istnieje tylko pięć wielościanów foremnych. Odpowiedź na to pytanie jest dość skomplikowana i związana jest z geometrią sferyczną. W skrócie, istnieje tylko pięć sposobów, w jaki sposób regularne wielokąty mogą spotkać się w wierzchołkach tak, aby suma kątów była mniejsza niż 360 stopni i wielościan był symetryczny.
Można również zauważyć, że liczba wierzchołków plus liczba ścian jest równa liczbie krawędzi plus dwa (to jest znane jako twierdzenie Eulera dla wielościanów).
Zastosowania i Wpływ
Wielościany foremne mają wiele zastosowań w różnych dziedzinach. Są podstawą dla wielu struktur w chemii i fizyce. Na przykład, cząsteczka metanu ma kształt czworościanu, a struktura krystaliczna diamentu jest oparta na sześcianie. W matematyce, wielościany foremne są często używane do ilustracji symetrii i innych właściwości geometrycznych.
Wielościany foremne miały również duży wpływ na sztukę i architekturę. Kształty te pojawiają się w wielu projektach od starożytnych czasów do dzisiaj.
Podsumowanie
Wielościany foremne są fascynującymi obiektami, które mają wiele zastosowań i wpływów na różne dziedziny. Choć z definicji są one dość proste, mają wiele ciekawych i skomplikowanych właściwości. Badanie tych pięciu unikalnych kształtów może dać nam ciekawe spojrzenie na matematykę, geometrię, a nawet na świat naturalny i sztukę.